Amplification#
Un problème fréquent du traitement de signal est l’amplification des signaux. Un système amplificateur est un élément qui applique sur un signal d’entrée un facteur d’amplification pour obtenir un signal de sortie plus grand (ou parfois plus petit, on parle alors d’atténuation).
Le schéma général d’un amplificateur est donné ci-dessous.
Fig. 1 Symbole générique d’un amplificateur#
Il existe plusieurs manières d’implémenter cette fonction. Dans le cadre de ce cours, nous n’allons étudier que l’amplification via un composant spécialement développé pour cela : l’amplificateur opérationnel.
Problématique de l’amplification#
Un amplificateur idéal a les caractéristiques suivantes :
Il est parfaitement linéaire : le signal en sortie est parfaitement proportionnel au signal en entrée, peu importe son point de fonctionnement (c’est-à-dire la valeur du signal en entrée ou du signal de sortie). Cette relation de proportionnalité est appelée le gain.
Il est parfaitement stable : le gain n’évoluera pas avec le temps, ne dépendra pas de la température, etc.
Il est parfaitement reproductible : deux amplificateurs identiques produisent exactement le même gain.
Note
Le gain évoqué au premier point des caractéristiques idéales peut par contre être dépendant de la fréquence (et c’est même souvent volontaire). En pratique, on parle de fonction de transfert : il s’agit de la relation entre le signal en entrée et le signal en sortie dans le domaine de Fourier en fonction de la fréquence. Dans un premier temps, nous considérerons ce gain comme constant et nous n’introduirons l’effet de la fréquence qu’au chapitre Fonctions de transfert.
Évidemment, les composants réels qui sont utilisés en électronique ne valident aucun des points ci-dessus. Mais pire que ça, ils peuvent avoir des dispersions de caractéristiques telles que leurs caractéristiques peuvent varier du simple au quadruple par exemple (pour 2 composants avec la même référence) []. Ces problèmes sont du même ordre de grandeur pour la stabilité et le point de fonctionnement. Il est donc impossible de faire un “bon” amplificateur avec des composants discrets (comme par exemple des transistors) sans utiliser de contre-réaction.
Principe de contre-réaction#
Pour pallier ces problèmes, on utilise un principe appelé la contre-réaction. Le principe est simple : on compare une partie du signal de sortie avec le signal d’entrée et on applique une correction pour que cette partie du signal de sortie soit le plus proche possible du signal d’entrée, de manière à ce que le gain final ne dépende (presque) pas des caractéristiques du composant amplificateur. Le schéma ci-dessous illustre ce principe. Il s’agit d’un schéma générique d’un système d’amplification avec contre-réaction.
Fig. 2 Schéma générique d’un amplificateur avec contre-réaction.#
Le principe de fonctionnement est le suivant:
Un facteur \(\alpha\) est appliqué au signal d’entrée \(V_{in}\)
Un facteur \(\beta\) est appliqué au signal de sortie \(V_{out}\)
Le signal \(\alpha V_{in}\) est comparé au signal \(\beta V_{out}\) pour former \(V_d = \alpha V_{in} - \beta V_{out}\) et la différence est amplifiée par un facteur \(A\) pour donner \(V_{out} = A V_d\).
On voit tout de suite ici que le système est bouclé : le signal de sortie est réinjecté dans le système après être inversé (par le signe -). C’est ce qui donne le nom de contre-réaction.
Le facteur \(\beta\) est appelé taux de réaction et correspond à la quantité du signal de sortie qui est ré-injecté dans le système. C’est une caractéristique très importante qui nous suivra tout le long de l’analyse des systèmes bouclés.
Mise en équation#
Le schéma général donné ci-dessus peut être résumé par le système d’équations suivant:
En remplaçant \(V_d\) par son expression, on obtient
Ce qui nous intéresse ici est le gain du système, défini comme \(V_{out}/V_{in}\). En isolant \(V_{out}\), on obtient
où l’approximation n’est valable que si \(A \beta \gg 1\).
Cette dernière remarque est très importante : elle signifie que si le gain interne \(A\) est très grand et que \(\alpha\) et \(\beta\) sont bien maitrisés, alors le gain total du système est très précis, même si \(A\) ne l’est pas du tout. C’est exactement ce qu’on recherche pour fabriquer un bon amplificateur. Il faudra donc trouver un moyen pour que ces 3 caractéristiques soient rencontrées.
Note
Pour que notre hypothèse sur \(\alpha\) et \(\beta\) précis soit valable, il faut impérativement que ces facteurs ne dépendent pas de composants actifs, toujours imprécis. \(\alpha\) et \(\beta\) seront donc toujours des atténuateurs dont la valeur sera inférieure ou égale à 1.
Erreur commise#
L’approximation proposée au paragraphe précédent génère une erreur sur le gain qu’il est important de quantifier afin d’évaluer la qualité d’un amplificateur. C’est ici l’erreur relative qui nous intéresse : elle est définie comme
La figure dynamique suivante permet de jouer avec les différents paramètres \(\alpha\), \(\beta\) et \(A\) pour comprendre leur impact sur le gain total du système et sa précision.
h
Fig. 3 Schéma générique d’un amplificateur avec contre-réaction.#
Il est intéressant de noter les points suivants (qui peuvent être expérimentés avec les différents paramètres de la figure):
Le paramètre \(\alpha\) a un impact direct sur le gain et n’a aucun impact sur l’erreur relative.
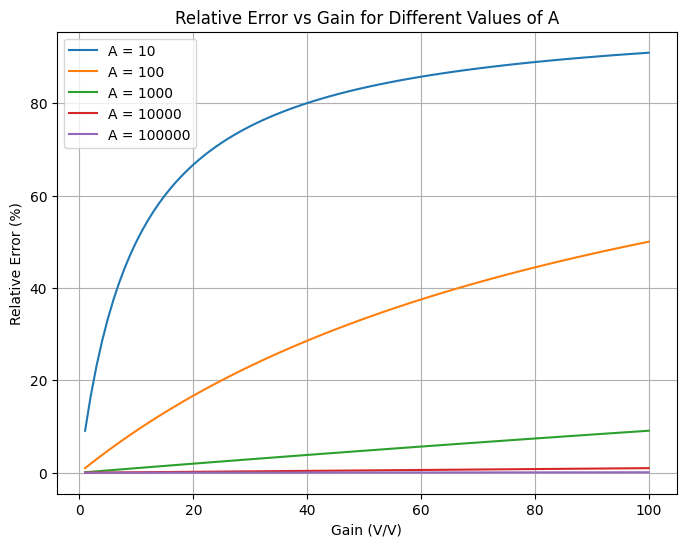
Si \(A\) est très grand (par exemple 100000), alors le gain est effectivement \(\alpha/\beta\) et l’erreur relative est très faible.
L’erreur relative augmente lorsque \(\beta A\) diminue, donc pour une valeur \(A\) donnée, plus le gain du système sera grand, plus l’erreur relative commise sera grande également.
Il est intéressant de noter que l’erreur commise provient du fait le gain idéal est évalué en considérant \(A = \infty\), et donc \(V_d = 0\). Or, en réalité, \(V_d\) doit être différent de 0 pour obtenir un signal en sortie. Il faut donc commettre une erreur en sortie pour générer un petit \(V_d\) qui permettra l’existance du signal de sortie. Forcément, plus \(A\) est grand, plus \(V_d\) doit être faible et donc plus l’erreur commise sera faible. En revanche, si le gain du système augmente, \(\beta\), qui est proportionnel à \(1/G\), diminue et il faut donc une plus grande erreur en sortie pour générer le même \(V_d\) (puisque \(\beta\) est le taux de réaction, donc la proportion du signal de sortie ré-injecté en entrée). Ce raisonnement explique intuitivement pourquoi l’erreur est dépendante du produit \(\beta A\).
Le graphique suivant reprend l’erreur commise en fonction du gain du système lorsque \(\alpha = 1\) et pour différentes valeurs de \(A\). On voit directement qu’on a intérêt à créer un système avec le \(A\) le plus grand possible pour minimiser l’erreur.
Amplificateur opérationnel#
Le système théorique décrit ci-dessus est extrêmement utilisé en électronique et c’est la raison pour laquelle les ingénieurs ont décidé de designer un composant spécifique pour remplir cette fonction : l’amplificateur opérationnel. Il s’agit d’un composant reprenant la fonctionnalité du soustracteur et de l’amplificateur du schéma général, habituellement représenté par un triange à 2 entrées et une sortie, comme représenté ci-dessous.
Fig. 4 Symbole de l’amplificateur opérationnel.#
Note
Jusqu’ici, tout le raisonnement proposé pour le système bouclé était parfaitement compatible avec n’importe quel système physique. Une fois qu’on commence à travailler avec un amplificateur opérationnel, le domaine se restreint à l’électronique.
Caractéristiques de l’amplificateur opérationnel idéal#
L’amplificateur opérationnel est un composant électronique dont le comportement n’est évidemment pas parfait. Cependant, dans un premier temps, nous allons définir une série de caractéristiques idéales que nous utiliserons pour étudier le comportement de l’amplificateur. Sous certaines conditions, cette approximation aura un impact tout à fait négligeable et le modèle sera donc valable. C’est ce qui sera fait ici. Il faudra ensuite étudier le domaine de validé de ces approximations.
Les caractéristiques idéales de l’amplificateur opérationnel sont les suivantes:
Le gain interme \(A\) est infini : \(A = \infty\), pour minimiser l’erreur commise sur le gain total du système.
L’impédance d’entrée est infinie : \(Z_{in} = \infty\), pour ne pas perturber le signal d’entrée.
L’impédance de sortie est nulle : \(Z_{out} = 0\), pour ne pas générer de chute de tension en sortie lorsqu’un courant est tiré.
En pratique, pour un amplificateur usuel, l’ordre de grandeur de ces valeurs est:
\(A \approx 100000\)
\(Z_{in} \approx 100M\Omega\)
\(Z_{out} \approx 100\Omega\)
Exemples de montage à amplificateur opérationnel#
Voici 2 exemples très courant de montage à amplificateur opérationnel. Il en existe énormément d’autres, capables de réaliser des fonctions bien plus large que la seule amplification.
Amplificateur non-inverseur#
Le premier exemple de montage est, comme son nom l’indique, un amplificateur. Il porte le nom de “non-inverseur” pour le différentier du prochain montage étudié.
Fig. 5 Amplificateur non-inverseur#
Pour étudier ce montage, 2 approches sont possibles.
Analyse par le schéma général#
Une première analyse (la plus polyvalente mais pas toujours la plus rapide et la plus simple) consiste à essayer de donner une valeur aux grandeurs \(\alpha\) et \(\beta\) du schéma général étudié ci-dessus. Une fois ces valeurs trouvées, il sera facile de trouver le gain.
Dans le cas de l’amplificateur non-inverseur, on voit directement que \(\alpha = 1\) (aucune modification n’est appliquée au signal d’entrée). En revanche, \(\beta\), qui correspond au taux de réaction (quantité de la sortie qui est ré-injectée en entrée) doit être calculé.
Ici, pour regarder l’effet de la sortie sur l’entrée \(-\), on peut appliquer le théorème de superposition. On met toutes les sources de tension à la masse et on voit directement qu’un pont diviseur est appliqué entre la sortie \(V_{out}\) et l’entrée \(-\). Par la formule du pont diviseur,
On obtient donc
Analyse par \(V_d=0\)#
Une autre approche plus rapide consiste à faire le racourci suivant: comme on considère l’amplificateur opérationnel comme idéal, on peut considérer également \(A = \infty\), et donc \(V_d = 0\). Comme expliqué précédement, cette hypothèse est correcte à condition que \(A \beta\) soit très grand. On a donc directement
et on obtient au final le même gain.
Amplificateur inverseur#
Le second exemple de montage est un amplificateur inverseur. Il porte ce nom car le signal de sortie est inversé par rapport au signal d’entrée (le gain est négatif).
Fig. 6 Amplificateur inverseur#
Il y a à nouveau 2 méthodes pour étudier ce circuit.
Analyse par le schéma général#
Comme pour l’amplificateur non-inverseur, on va tenter d’identifier les valeurs de \(\alpha\) et \(\beta\) pour ensuite trouver le gain. Dans ce cas, il n’est plus vrai que \(\alpha = 1\) : le signal d’entrée va être “mixé” au signal de sortie et sera donc modifié. Pour déterminer la valeur de \(\alpha\), on peut appliquer le théorème de superposition en ne gardant que \(V_{in}\) comme source de tension. On obtient alors
Le signe négatif est dû au fait que le signal est appliqué sur l’entrée \(-\) de l’amplificateur opérationnel (donc sur la branche “soustractive” du schéma général).
Pour obtenir \(\beta\), on peut appliquer le même raisonnement que pour l’amplificateur non-inverseur, et donc toujours par superposition, on obtient
Pour finir, le gain du système est donné par
Analyse par \(V_d=0\)#
Comme pour l’amplificateur non-inverseur, on peut également faire l’hypothèse \(V_d = 0\) et donc \(V^+ = V^-\). Dans ce cas, quelque chose d’important se passe: comme \(V^+\) est relié à la masse, le système va se “battre” pour que la tension de \(V^-\) se retrouve à 0V, sans pour autant avoir de courant qui puisse circuler entre ce point et la masse. On parle alors de masse virtuelle. Grâce à cette observation, on connait le courant qui circule dans \(R_1\):
Comme on a fait l’hypothèse que l’impédance d’entrée de l’amplificateur opérationnel était infinie, aucun courant ne rentre dans l’entrée \(-\). On a donc le même courant qui circule dans \(R_2\) et ce courant génère une différence de tension
ce qui nous donne le même gain que précédemment. Le signe \(-\) provient du fait que la tension est toujours mesurée par rapport à la masse et que le courant circule de la masse vers la sortie, donc automatiquement la tension est inversée.
