Interpretation du diagramme de Bode#
Le diagramme de Bode est un outil graphique permettant de représenter la réponse fréquentielle d’un système (c’est-à-dire le comportement d’un système à une fréquence d’entrée donnée). Il est composé de deux graphiques :
Un graphique en échelle logarithmique de la fréquence en abscisse et du gain en décibels en ordonnée
Un graphique en échelle logarithmique de la fréquence en abscisse et du déphasage en degrés en ordonnée.
Ce graphique permet d’identifier rapidement les caractéristiques importantes de la fonction de transfert (fréquences de coupure, gain en pleine bande, etc.).
Il n’est cependant pas aisé de tracer à la main ce diagramme de Bode, ni de tirer des conclusions des fonctions de transfert. C’est la raison pour laquelle le comportement asymptotique du diagramme de Bode est intéressant.
Comportement asymptotique#
Le comportement asymptotique consiste à simplifier le diagramme de Bode pour ne tracer que des droites. C’est évidemment une approximation mais elle est très utile pour développer une intuition sur les fonctions de transfert.
Exemple d’un filtre passe-bas#
Prenons l’exemple de la fonction de transfert d’un filtre passe-bas formé par un circuit RC (2).
Pour interpreter un tel filtre, on découpe le domaine fréquentiel en 2 zones :
La zone des basses fréquences ou \(|j\omega RC| < 1\).
La zone des hautes fréquences ou \(|j\omega RC| > 1\).
Ces 2 zones sont séparées par une pulsation appelée pulsation de coupure \(\omega_c = \frac{1}{RC}\), puisque \(|j \omega_c RC| = 1\).
La raison pour laquelle on fait cette découpe est que dans chaque zone, on va considérer uniquement le terme le plus grand (en valeur absolue) du dénominateur et négliger l’autre. Ceci est évidemment une bonne approximation lorsqu’on est très loin de \(\omega_c\) et devient de plus en plus mauvaise à mesure qu’on se rapproche de \(\omega_c\).
Basse fréquence#
En basse fréquence (avec \(\omega < \omega_c\)), on peut donc faire l’approximation suivante (en considérant que \(|j\omega RC| << 1\)) :
En conclusion, on approxime la fonction de transfert à 1 lorsque \(\omega < \omega_c\) (donc le filtre est inactif à ces fréquences).
Haute fréquence#
En haute fréquence (avec \(\omega > \omega_c\)), on peut faire l’approximation suivante (en considérant que \(|j\omega RC| >> 1\)) :
On voit donc que le gain est inversément proportionnel à la fréquence et que le déphasage est de -90°. Puisque le gain est inversément proportionnel à la fréquence, chaque fois que la fréquence est multipliée par 10, le gain est divisé par 10. On dit que le gain diminue de -20dB/décade (puisque par définission, -20dB = \(1/10\)).
Représentation graphique#
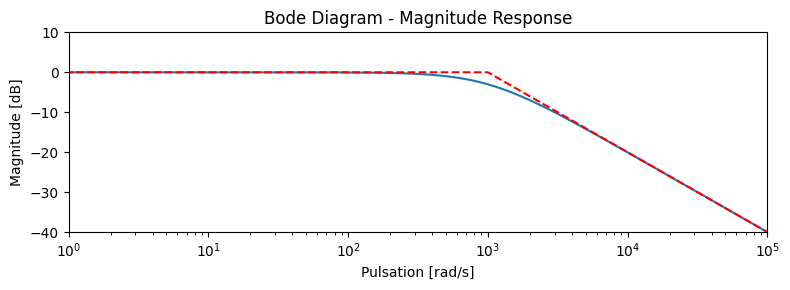
Sur base des conclusions précédentes, on peut représenter le diagramme de Bode asymptotique du filtre RC passe-bas par le diagramme ci-dessous (avec ici \(R=1k\Omega\) et \(C=1 \mu F\)).
En bleu est représentée la courbe réelle de la fonction de transfert, en rouge la courbe asymptotique. On remarque que comme prévu, l’approximation est de très bonne qualité lorsqu’on s’éloigne de la pulsation de coupure \(\omega_c = 1000 \\ rad/s\).
Exemple d’un filtre passe haut#
Un raisonnement tout à fait similaire permet de conclure que le diagramme de Bode asymptotique d’un filtre passe-haut avec comme fonction de transfert (1)
est décrit comme suit :
Il a une fréquence de coupure \(\omega_c = \frac{1}{RC}\).
En basse fréquence (avec \(\omega < \omega_c\)), la fonction de transfert est approximée par
et son gain croit de 20dB/décade avec un déphasage est de +90°.
En haute fréquence (avec \(\omega > \omega_c\)), la fonction de transfert est approximée par
et le déphasage est de 0°.
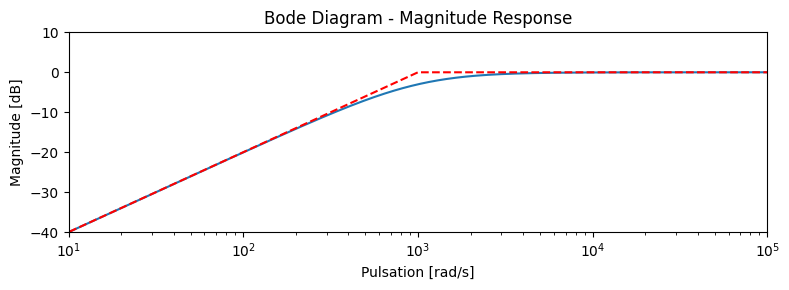
On peut donc tracer son diagramme de Bode asymptotique comme suit (avec \(R=1k\Omega\) et \(C=1 \mu F\)).
Cas général#
Le cas général d’une fonction de transfert \(T(\omega)\) est plus complexe mais peut être également simplifié grâce à l’approche asymptotique. Une fonction de transfert \(T(\omega)\) d’un système linéaire peut toujours être réécrite sous la forme
En d’autre terme, le numérateur et le dénominateur peuvent être décomposés comme un produit de termes du premier ordre. Il est donc possible de décomposer la fonction de transfert comme un produit de fonctions de transfert du premier ordre :
où chaque \(T_i(\omega)\) est de la forme
\(T_i(\omega) = \frac{1}{1 + j\frac{\omega}{\omega_{zi}}}\) ou
\(T_i(\omega) = 1 + j\frac{\omega}{\omega_{pi}}\).
Or, ces 2 formes de fonction de transfert ont déjà été étudiées de manière asymptotique : la première représente la famille des filtres passe-haut de premier ordre et la seconde la famille des filtres passe-bas du premier ordre.
Comme un produit se transforme en addition dans le monde logarithmique (qui est le monde utilisé par la représentation des diagrammes de Bode), il suffit donc d’addition les représentations des différentes fonctions de transfert pour obtenir le diagramme de Bode de la fonction de transfert générale.
Exemple d’un filtre passe-bande#
Prenons l’exemple du circuit ci-dessous:
Pour étudier ce circuit, nous allons faire l’approximation que le filtre passe-haut formé par \(R_1\)-\(C_1\) a une fréquence de coupure très supérieure au filtre passe-bas formé par \(R_2\)-\(C_2\). Cela nous permet de considérer chaque filtre séparément en considérant que chaque filtre est inactif lorsque l’autre est actif. Ceci est évidemment d’autant plus vrai que les fréquences de coupure sont éloignées.
Dans le cas de l’hypothèse précédente, la fonction de transfert peut être approximée comme le produit des fonctions de chaque filtre:
L’analyse asymptotique nous donne donc 3 domaines différents puisque la fonction de transfert (exprimée en dB) est la somme des 2 fonctions de transferts:
En basse fréquence (\(\omega\) < \(1/(R_2 C_2)\)): le filtre passe bas est inactif et le filtre passe-haut nous donne un gain qui grandit de 20dB par décade
En pleine bande (\(1/(R_1 C_1)\) < \(\omega\) < \(1/(R_2 C_2)\)): aucun des 2 filtres n’est actif et le gain est de 1
En haute fréquence (\(\omega\) > \(1/(R_1 C_1)\)): le filtre passe bas est inactif et le filtre passe-haut nous donne un gain qui décroit de 20dB par décade
Nous obtenons le diagramme de Bode suivant pour une pulsation de coupure basse \(1/(R_1 C_1) = 1kHz\) et une pulsation de coupure haute de \(1/(R_2 C_2) = 10 kHz\).
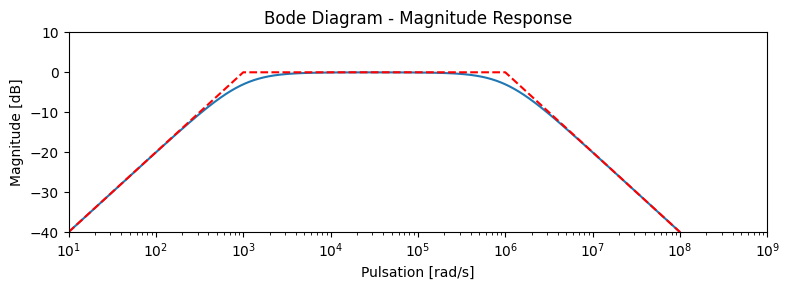
Comme dit plus tôt, le résultat de l’analyse asymptotique est très proche du diagramme de Bode réel (en bleu) parce que les fréquences de coupure sont fortement éloignées (il y a un facteur 1000 entre les 2) et donc la simplification a très peu d’impact.
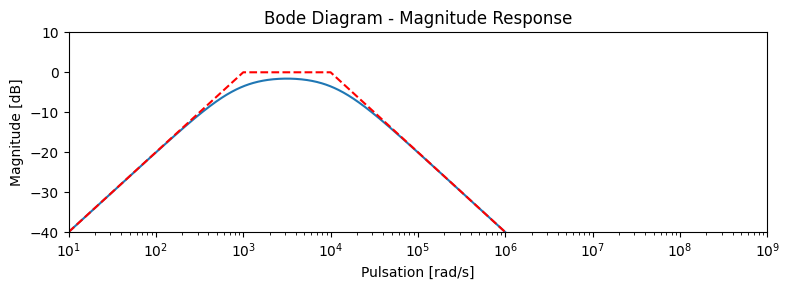
Mais en réduisant l’écart entre les fréquences de coupure, la simplification devient mauvaise, comme illustrée par l’exemple ci-dessous ou le facteur entre les 2 fréquences de coupure est de 10.
Note
La fonction de transfert réelle est différente de notre approximation puisqu’elle doit prendre en compte le courant traversant le 2ème filtre lors de l’analyse du premier. On obtient alors des fréquences de coupures réelles données ci-dessous. Évidemment, pour des fréquences de coupure très éloignées, on retrouve \(1/(R_1C_1)\) et \(1/(R_2C_2)\), ce qui est évidemment préférable devant l’horreur calculatoire ci-dessous.
