Limite en fréquence d’un amplificateur opérationnel

Jusqu’à présent, les amplificateurs opérationnels ont été considérés comme parfait (Gain différentiel infini, impédance d’entrée infinie, impédance de sortie nulle, etc). Ce modèle est évidemment limité aux cas “qui vont bien” et l’étude des cas “qui vont mal” est indispensable pour trouver la limite entre ces 2 mondes.

La limite étudiée ici est la limite en fréquence d’un amplificateur opérationnel.

Origine de la limite en fréquence

L’origine physique de la limite en fréquence vient d’un filtre passe-bas ajouté volontairement par les constructeurs à l’intérieur de l’amplificateur opérationnel pour éviter des problèmes d’instabilité à haute fréquence. L’explication détaillée de l’origine de ces instabilités et de la manière dont le filtre passe-bas les évite est hors du cadre de ce cours.

Ce qu’il faut cependant retenir est que le modèle de notre amplificateur opérationnel doit être modifié pour tenir compte de ce filtre passe-bas et évaluer comment il peut devenir problématique.

Un nouveau modèle plus proche de la réalité est présenté sur la figure ci-dessous. Le premier élément représente un amplificateur opérationnel idéal, le second le filtre et le dernier représente un buffer qui assure l’hypothèse d’impédance de sortie nulle.

En pratique, le filtre passe-bas n’est pas réalisé par un filtre RC mais cela a peu d’importance puisque l’important est qu’il se comporte de la même manière. Cela n’a donc pas de sens de donner une valeur pour R et pour C. Ce qui nous intéresse en revanche est la pulsation de coupure \(\omega_c\) de ce filtre. Elle peut être retrouvée dans la datasheet (même si elle ne sera pas présentée sous cette forme).

Le gain différentiel de l’amplificateur opérationnel est donc dépendant de la fréquence et peut être exprimé sous la forme d’une fonction de transfert:

\[A(\omega) = A_{DC} \frac{1}{1 + j\frac{\omega}{\omega_c}},\]

où \(A_{DC}\) représente le gain à basse fréquence.

Note

Ça n’a aucun sens de garder l’hypothèse du gain infini lors de l’analyse de la limite en fréquence, puisqu’alors, \(A(\omega)\) vaut également l’infini.

Impact de la limite en fréquence

En reprenant le schéma général du système d’amplification avec feedback négatif donné ci-dessous, on sait que la fonction de transfert totale du système est donnée par

\[T(\omega) = \alpha \frac{A(\omega)}{1 + A(\omega) \beta}.\]

Pour évaluer la fonction de transfert ci-dessus, il faut donc remplacer \(A(\omega)\) par son expression donnée plus haut. On obtient alors

\[T(\omega) = \alpha \frac{A_{DC} \frac{1}{1 + j\frac{\omega}{\omega_c}}}{1 + A_{DC} \frac{1}{1 + j\frac{\omega}{\omega_c}} \beta}.\]

En multipliant le numérateur et le dénominateur par \(1 + j \omega / \omega_c\), on obtient

\[T(\omega) = \alpha \frac{A_{DC}}{1 + j\frac{\omega}{\omega_c} + A_{DC} \beta}.\]

Comme 1 est très inférieur à \(A_{DC} \beta\), on peut le négliger et on obtient finalement

\[T(\omega) \approx \alpha \frac{A_{DC}}{j\frac{\omega}{\omega_c} + A_{DC}\beta} = \alpha \frac{1}{j \frac{\omega}{\omega_c A_{DC}} + \beta} = \frac {\alpha}{\beta} \frac{1}{j \frac{\omega}{\omega_c A_{DC} \beta} + 1} = T_{DC} \frac{1}{j \frac{\omega}{\omega_{TA} \beta} + 1},\]

où \(\omega_{TA}\) est défini comme \(\omega_c A_{DC}\) et est appelée la fréquence de transition. C’est une caractéristique propre à l’amplificateur opérationnel qui se trouve dans sa datasheet (puisque \(\omega_c\) est la fréquence de coupure intrinsèque de l’amplificateur opérationnel).

On peut donc en conclure qu’en tenant compte de la limite en fréquence, le système se comporte comme un amplificateur avec un gain donné \(T_{DC}\) suivit d’un filtre passe-bas avec une pulsation de coupure donnée par \(\omega_{TA} \beta\).

Il y a donc un compromis à trouver entre gain et bande passante. Cependant, une solution simple pour augmenter la bande passante sans diminuer le gain est la réalisation d’un amplificateur à plusieurs étages. Ainsi, le gain peut être réparti sur les différents étages en gardant un \(\beta\) suffisamment élevé pour garantir la bande passante voulue.

Note

La fréquence de transition tire son nom d’une de ses caractéristiques: c’est également la fréquence à laquelle le gain est nul. En d’autres termes, avant cette fréquence, le circuit agit comme un amplificateur (\(|A(\omega)| > 1\)) et après comme un atténuateur (\(|A(\omega)| < 1\)).

Ceci se démontre car

\[A(\omega_{TA}) = \frac{A_{DC}}{1 + j\frac{\omega_{TA}}{\omega_c}} = \frac{A_{DC}}{1 + j\frac{\omega_c A_{DC}}{\omega_{c}}} = \frac{A_{DC}}{1 + j A_{DC}} \approx \frac{1}{j} = -j,\]

puisqu’en norme, \(|j A_{DC}| >> 1\).

Exemples

Amplificateur inverseur

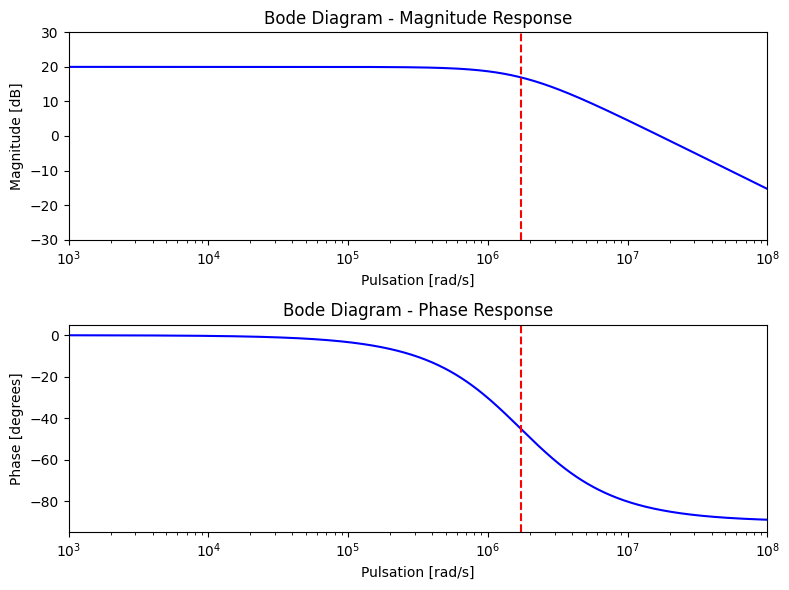
Le schéma ci-dessous représente un amplificateur inverseur avec un gain de 10 réalisé avec un amplificateur opérationnel dont la datasheet nous indique un \(f_{TA} = 3MHz\) (donc \(\omega_{TA} = 2\pi \times 3 \times 10^6\)).

Le taux de contre-réation est donné par \(\beta = \frac{R_1}{R_1 + R_2} = 1/11\) et nous avons donc une fréquence de coupure donnée à

\[f_{c} = f_{TA} \frac{1}{11} = 272.72 kHz.\]

Son diagramme de Bode est donné ci-dessous.