Exemple de filtres#
Voici la présentation et l’analyse de quelques filtres courants utilisés dans le cadre de l’amplification en tension.
Amplificateur inverseur avec filtre passe-haut#
Le schéma ci-dessous représente un circuit jouant le rôle d’amplificateur inverseur et de filtre passe-haut.
Analyse mathématique#
Ce qui a déjà été déduit du comportement de l’amplificateur opérationnel en montage inverseur peut être généralisé au cas d’une impédance complexe en lieu et place de la résistance entre \(V_{in}\) et l’entrée \(-\). On obtient donc comme fonction de transfert
où \(Z_1\) représente la résistance \(R_1\) et le condensateur en série.
En factorisant \(R_1\) au dénominateur, on obtient la fonction de transfert suivante:
On peut donc écrire la fonction de transfert comme le produit de 2 fonctions:
\(R_2/R_1\) : une fonction de transfert constante qui ne dépend pas de la fréquence et qui représente le gain d’un amplificateur inverseur sans filtre
\(\frac{1}{1 + 1/(j\omega R_1 C)}\) : une fonction de transfert qui dépend de la fréquence et qui correspond à celle d’un filtre passe-haut.
On peut donc conclure que le circuit se comporte exactement comme un filtre passe-haut dont le gain à haute fréquence est de \(R_2/R_1\) au lieu de 1.
Diagramme de Bode#
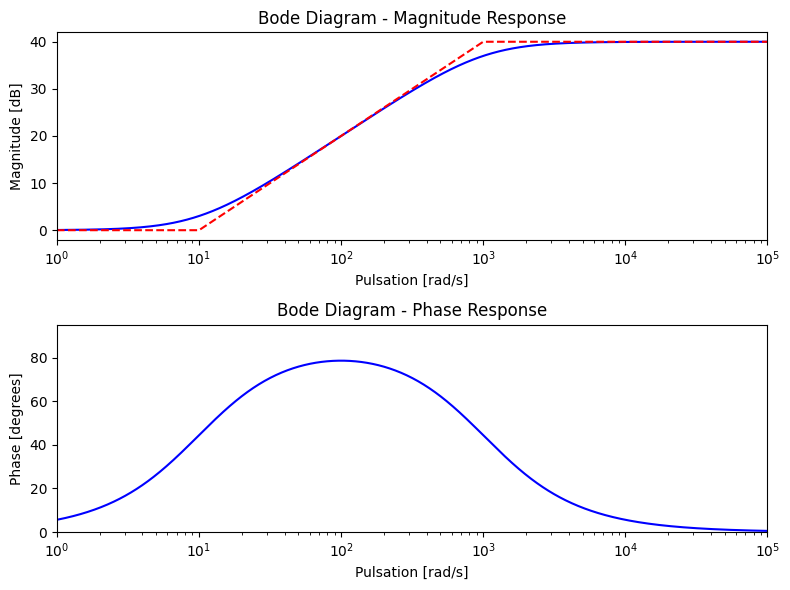
Étant donné ce qui a été décrit ci-dessus, le diagramme de Bode du circuit est celui du filtre passe-haut classique relevé de \(R_2/R_1\) exprimé en dB. Voici un exemple de diagramme de Bode avec \(R_1=1\,\text{k}\Omega\), \(R_2=10\,\text{k}\Omega\) et \(C=1\,\mu\text{F}\). Sur ce diagramme,
la courbe verte représente le filtre passe-haut seul
la courbe bleue représente le filtre passe-haut avec l’amplificateur inverseur
On remarque que
L’amplitude est bien relevée de 20 dB (puisque le gain est de 10).
Le déphasage à la même allure mais est décalé de 180°. Ce déphasage provient du signe \(-\) devant le gain de l’amplificateur inverseur.
Amplificateur non-inverseur avec filtre passe-haut#
Le schéma ci-dessous représente un circuit jouant le rôle d’amplificateur non-inverseur et de filtre passe-haut.
Note
Ce circuit est très précieux : il permet de conserver la composante DC sans l’amplifier tout en apportant un gain au signal utile, comme nous allons le démontrer.
Analyse mathématique#
En repartant de la fonction de transfert connue de l’amplificateur non-inverseur, on peut écrire la fonction de transfert du circuit comme
avec \(Z_2\) représentant la résistance \(R_2\) et le condensateur en série.
En divisant le numérateur et le dénominateur par \(R_2\), on obtient
avec \(T_{\infty}\) qui représente le gain du circuit à très haute fréquence (donc sans filtre).
Analyse asymptotique#
La forme donnée ci-dessus n’est pas aussi séduisante que celle de l’amplificateur inverseur, et il est difficile d’en tirer des conclusions. Cependant, si on fait l’hypothèse que \(T_{\infty} >> 1\), on peut découper le domaine fréquentiel en 3 zones bien distinctes:
A très basse fréquence (\(1/j\omega R_2 C >> T_{\infty} >> 1\)), le circuit a un gain de 1
A moyenne fréquence (\(1 << 1/j\omega R_2 C << T_{\infty}\)), le numérateur est dominié par \(T_{\infty}\) et mais le dénominateur est dominé par \(1/j\omega R_2 C\). Le gain croit donc de linéairement avec la fréquence (de 20dB par décade)
A haute fréquence (\(T_{\infty} >> 1 >> 1/j\omega R_2 C\)), le circuit a un gain de \(T_{\infty}\).
Note
Il n’est possible d’obtenir le domaine de moyenne fréquence que si \(T_{\infty} >> 1\), d’où l’importance de notre hypothèse de départ.
Il y a donc 2 points de basculement (transition entre un comportement asymptotique et un autre):
\(\omega_{c_1} = 1/(R_2 C T_{\infty})\), on passe du gain unitaire à l’acroissement de 20dB par décade
\(\omega_{c_2} = 1/(R_2 C)\), on passe de l’acroissement de 20dB par décade à un gain de \(T_{\infty}\).
Diagramme de Bode#
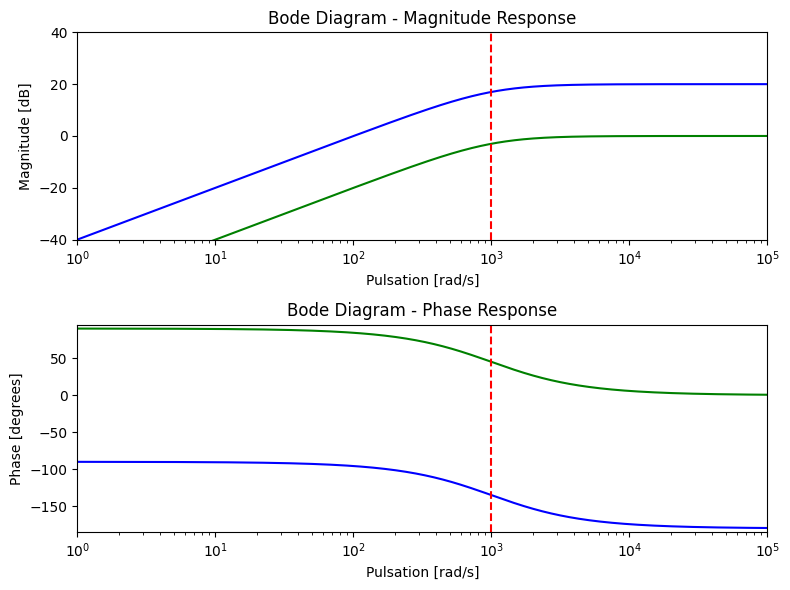
Voici le diagramme de Bode réel et asymptotique de ce filtre avec
\(R_1 = 99k\Omega\)
\(R_2 = 1k\Omega\)
\(C = 1\mu F\)
On obtient donc