Fonctions de transfert

La fonction de transfert est un outil précieux pour modéliser le comportement des systèmes physiques lors de l’application d’un signal d’entrée. Cet outil est applicable à tous les domaines de la physique et de l’ingénieurie pour peu qu’ils soient linéaires.

Note

L’étude des fonctions de transfert se fait habituellement dans le domaine de Laplace, beaucoup plus adapté à l’étude de stabilité (pour la régulation par exemple). Cependant, pour nous travaillerons ici dans le domaine de Fourier par simplicité. Tous les raisonnements utilisés ici sont valables dans les 2 domaines.

Avant de rentrer dans le détail, commençons par un exemple pour illustrer l’intérêt de ces outils.

Important

Dans toute l’analyse décrite ci-dessous (et chaque fois qu’une fonction de transfert peut être utilisée), il est important de noter que les systèmes ne modifier jamais les fréquences présentes. Si une sinusoïde de fréquence \(f\) est appliquée en entrée, la sortie sera toujours une sinusoïde de fréquence \(f\) (même si l’amplitude et la phase peuvent être modifiées).

Ceci s’applique évidemment pour n’importe quelle fonction. Par exemple, si l’entrée est un signal carré de fréquence \(f_0\), il sera composé d’une somme infinie de fréquences \(f_i\). Dans ce cas, la sortie sera également composée de ces mêmes fréquences \(f_i\) (même si certaines pourraient avoir une amplitude nulle et donc ne plus faire partie du signal de sortie). Dans tous les cas, aucune fréquence ne sera ajoutée ou modifée.

Système masse-ressort

Pour expliquer l’intérêt des fonctions de transfert, partons de l’exemple très simple (et très loin de l’électronique) d’un système masse-ressort.

Le système consiste en une masse \(m\) attachée à un ressort de raideur \(k\). L’autre extrémité du ressort est soumise à un mouvement d’excitation suivant une fonction périodique \(f(t)\). Nous négligeons ici les forces de frottement et la gravité. Le système peut être modélisé par l’équation différentielle suivante :

\[p(t) = m \ddot{x}(t) = - k [x(t) - f(t)],\]

où \(x(t)\) est la position de la masse par rapport à sa position d’équilibre, \(p(t)\) est la force exercée par le ressort sur la masse et \(\ddot{x}(t)\) est la dérivée seconde de \(x(t)\) par rapport au temps (donc l’accélération de la masse). Cette équation vient simplement du fait que par définition de la raideur d’un ressort, la force appliquée par le ressort et proportionnelle à l’élongation du ressort.

En prenant \(f(t)=0\), cette équation différentielle est évidemment bien connue et offre une famille de solutions du type \(x(t) = A \cos(\omega t + \phi)\), où \(A\) est l’amplitude de l’oscillation, \(\omega\) est la pulsation de l’oscillation et \(\phi\) est la phase de l’oscillation. \(\omega\) sera déterminé par \(m\) et \(k\) alors que \(A\) et \(\phi\) dépendront des conditions initiales.

Mais le cas qui nous intéresse est plus compliqué puisque \(f(t)\) n’est pas nul. Pour résoudre cette équation, nous allons utiliser la transformée de Fourier.

Pour rappel, la transformée de Fourier de la dérivée d’une fonction \(g\) (écrite \(\mathcal{F}(\dot g)\)) est simplement donnée par \(j \omega \mathcal{F}(g)\). L’équation différentielle devient donc simplement dans le domaine de Fourier

\[m (j \omega)^2 X(\omega) = - k (X(\omega) - F(\omega)),\]

où \(X(\omega)\) est la transformée de Fourier de \(x(t)\) et \(F(\omega)\) est la transformée de Fourier de \(f(t)\). Pour étudier l’impact d’un système linéaire sur son signal d’entrée, il est intéressant d’évaluer le rapport entre la sortie et l’entrée. Ce rapport est appelé fonction de transfert et est défini comme \(X(\omega)/F(\omega)\) (le rapport entre la transformée de Fourier de la sortie et la transformée de Fourier de l’entrée). Dans le cas de notre système, on obtient

\[\frac{X(\omega)}{F(\omega)} = T(\omega) = \frac{k}{m (j \omega)^2 + k} = \frac{k}{-m \omega^2 + k}.\]

Mais que peut-on conclure de ça ? Pour le savoir, il est intéressant de tracer le diagramme de Bode de cette fonction de transfert. Il s’agit de représenter l’amplitude et la phase de la fonction de transfert en fonction de la pulsation. Cela permet de savoir comment le système réagit à une excitation de fréquence donnée.

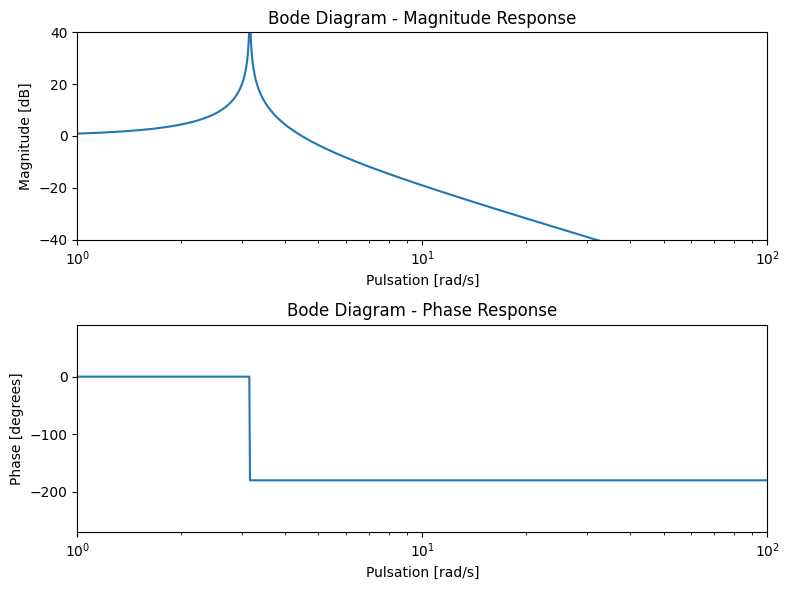
Le diagramme de Bode nous montre quatre choses intéressantes:

• A basse fréquence, la fonction de transfert est proche de 1 et le déphasage est nul. Cela signifie que le système suit de près l’excitation.

• Il existe une fréquence donnée par \(\sqrt{(k/m)}\) où la fonction de transfert atteint l’infini. C’est la fréquence de résonance du système. A cette fréquence, il peut exister un signal périodique même si l’excitation est nulle. C’est exactement le cas de la solution de l’équation différentielle sans excitation décrite plus haut.

• Au-delà de la fréquence de résonance, la fonction de transfert décroît en amplitude et le déphasage est de 180°. Cela signifie que la masse oscillera en opposition de phase par rapport à l’excitation.

• A très haute fréquence, l’amplitude de la fonction de transfert tend vers 0. La masse ne bouge donc (quasiment) plus.

Les animations suivantes nous montrent le comportement du système à ces différents endroits.

Note

En pratique, évidemment la fonction \(f(t)\) ne sera pas une simple sinusoïde comme dans les exemples ci-dessous. Cependant, il est possible de décomposer n’importe quelle fonction périodique en une somme de sinusoïdes (comme nous le démontre le théorème de Fourrier). Il est donc possible de comprendre le comportement du système pour une excitation donnée en observant son comportement pour des sinusoïdes. Le comportement du système pour une excitation quelconque sera alors la somme des comportements pour chaque sinusoïde (tant qu’il reste linéaire).

À basse fréquence

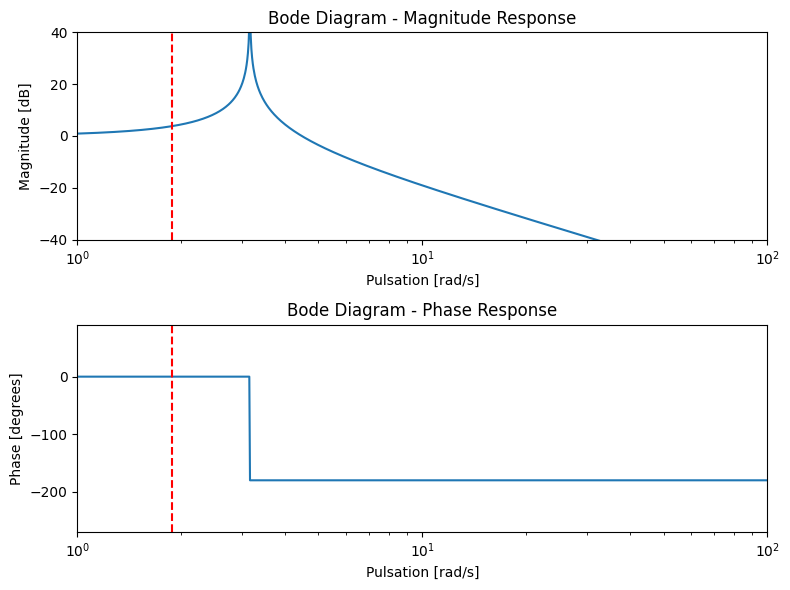
Proche de la fréquence de résonance

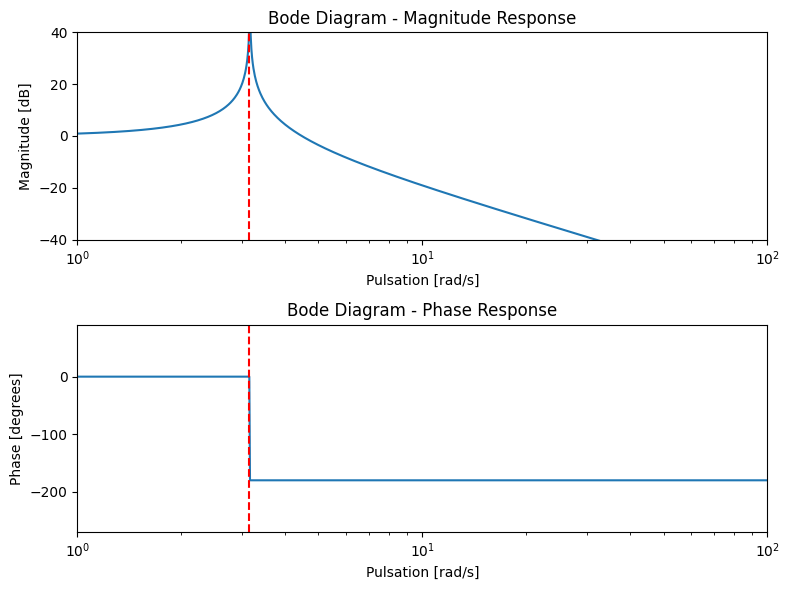
Au delà de la fréquence de résonance

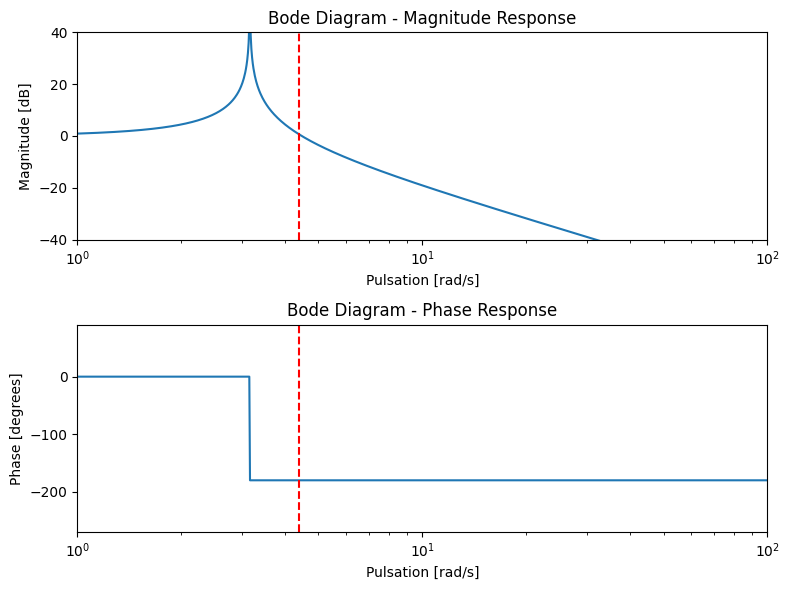
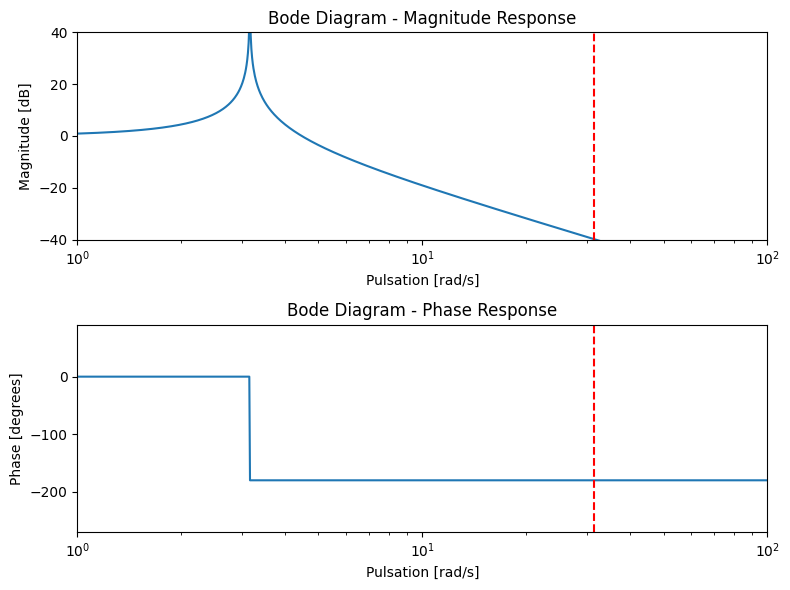
À haute fréquence

Note

Il est évident que l’analyse ci-dessus n’est valide que tant que le système reste linéaire. En pratique, si l’amplitude de l’oscillation de sortie devient trop grande, le système quitteras la zone linéaire pour arriver dans une zone de saturation. Dans le cas du ressort, la saturation peut prendre différentes formes dont voici une série d’exemples:

• Le ressort est compressé au maximum

• Le ressort est détendu au maximum

• Le ressort casse

• La masse touche le sol ou le plafond

L’étude de la fonction de transfert doit donc se faire en tenant compte des limites du système et ces limites doivent être évaluées indépendamment.

Cas d’un filtre RC passe-haut

Tout le raisonnement décrit ci-dessus s’applique à n’importe quel système physique, y compris les systèmes électroniques. Nous allons ici étudier le cas classique du filtre RC. Le schéma du filtre RC passe-haut est donné ci-dessous.

Pour déterminer la fonction de transfert de ce système, nous allons également partir de l’équation différentielle. Puisque tout le courant qui passe dans la résistance \(R\) charge ou décharge \(C\) (en faisant l’hypothèse que la résistance d’entrée de l’étage suivant est infinie), on a l’équation suivante:

\[C (\frac{dv_i}{dt}(t) - \frac{dv_o}{dt}(t)) = C \frac{dv_C}{dt}(t) = i_C(t) = \frac{v_o(t)}{R},\]

avec \(v_C(t)\) la tension aux bornes de la capacité. En passant dans le domaine de Fourier, cette équation devient

\[j \omega C (V_i(\omega) - V_o(\omega)) = V_o(\omega) R,\]

ce qui donne après transformation

(1)\[\frac{V_o(\omega)}{V_i(\omega)} = T(\omega) = \frac{j\omega C R}{1 + j \omega R C} = \frac{1} {1 + \frac{1}{j \omega R C}}.\]

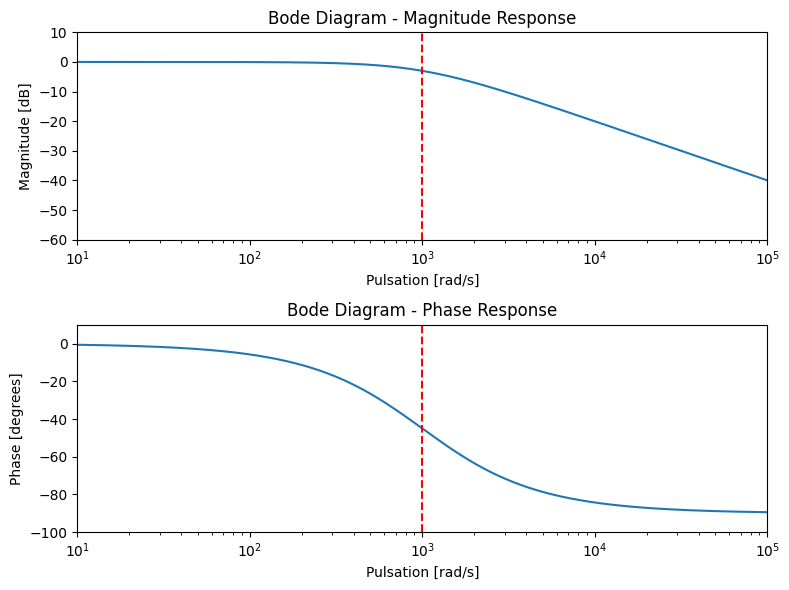
Le diagramme de Bode de cette fonction de transfert est donné ci-dessous (avec \(R = 1k\Omega\) et \(C=1 \mu F\)).

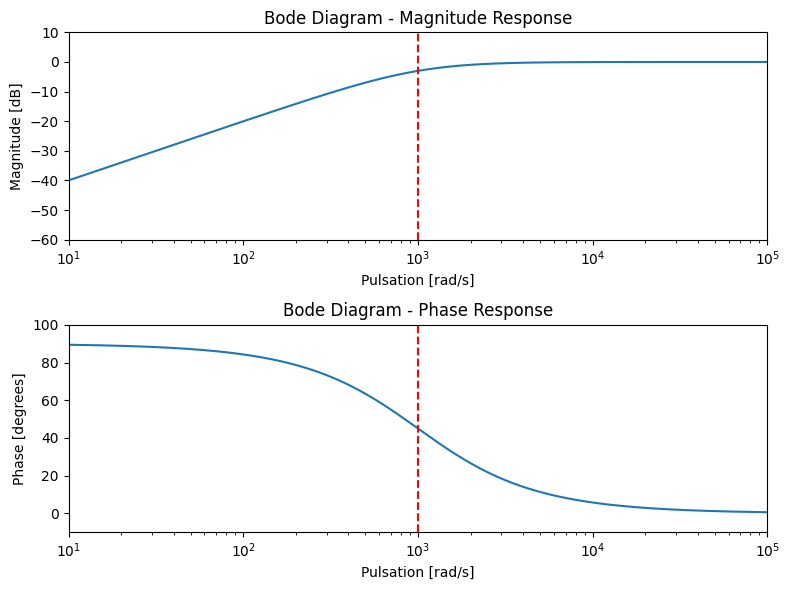
Fonction de transfert des éléments R, L et C

Le raisonnement décrit précédemment est lourd et complexifie l’analyse. Or, si nous connaissons la fonction de transfert des différents éléments de base d’un ciruit électrique (R, L et C), on gagnera énormément de temps.

Dans le cas de ces éléments, la grandeur physique en entrée (un courant) n’est pas la même que la grandeur en sortie (une tension), mais cela ne change rien au raisonnement.

Fonction de transfert d’une résistance

Nous savons qu’une résistance respecte \(u(t) = R i(t)\). Puisque la transformée de Laplace est linéaire, ceci reste vrai dans le monde de Fourier (donc \(U(s) = R I(s)\)). La fonction de transfert est donc simplement

\[T(\omega) = R.\]

Fonction de transfert d’une self-inductance

L’équation qui décrit le comportement d’une self est

\[ u(t) = L \frac{di(t)}{dt}.\]

En passant de le domaine de Fourier, on obtient donc

\[U(\omega) = L j\omega I(\omega),\]

et sa fonction de transfert est donc

\[T(\omega) = j \omega L.\]

Fonction de transfert d’une capacité

L’équation qui décrit le comportement d’une capacité est

\[i(t) = C \frac{du(t)}{dt}.\]

En passant de le domaine de Fourier, on obtient donc

\[I(\omega) = C j\omega U(\omega),\]

et sa fonction de transfert est donc

\[T(\omega) = \frac{U(\omega)}{I(\omega} = \frac{1}{j \omega C}.\]

Analyse du filtre RC passe bas

Nous allons maintenant étudier le filtre RC passe-bas. Le schéma du filtre RC passe-bas est donné ci-dessous.

Pour déterminer sa fonction de transfert, nous allons nous simplifier la vie en utilisant directement toutes les fonctions de transfert des composants linéaires. On peut simplement appliquer la formule du pont diviseur pour obtenir

(2)\[T(\omega) = \frac{Z_C(\omega)}{Z_R(\omega) + Z_C(\omega)} = \frac{\frac{1}{j \omega C}}{R + \frac{1}{j \omega C}} = \frac{1}{1 + j \omega R C}.\]

On obtient alors le diagramme de Bode ci-dessous pour \(R = 1k\Omega\) et \(C = 1 \mu F\).